Salam Para Bintang
Kali ini kita akan membahas materi tentang materi dasar untuk mempersiapkan diri di ujian UTBK, Ujian Sekolah, Ujian Masuk PTN lainnya. Materi ini adalah sangat muncul dalam berbagai soal-soal ujian yang diadakan apalgi mau masuk PTN. Jadi, sebelum kalian menyelesaikan soal-soal kedudukan dua lingkaran fungsi, maka pastinya pahami dulu materinya ya. Oke !
A. Kedudukan Dua Lingkaran
Kedudukan dua lingkaran meninjukkan bagaimana posisi dari lingkaran pertama dengan lingkaran kedua. Hubungan (kedudukan) dua lingkaran terdiri atas empat kemungkinan yaitu:
1. Tidak Berpotongan, tetapi di luar sesamanya
Perhatikan gambar berikut!

Dari gambar di atas, menunjukkan bahwa lingkaran 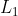 dengan jari-jari
dengan jari-jari 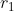 dan lingkaran
dan lingkaran 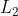 dengan jari-jari
dengan jari-jari  , dimana
, dimana 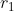 >
>  . Misalkan d = jarak pusat lingkaran
. Misalkan d = jarak pusat lingkaran 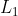 dan
dan 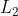 .
.

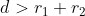
Jadi, jika 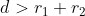 maka lingkaran
maka lingkaran 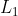 dan
dan 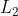 tidak berpotongan, tetapi di luar sesamanya.
tidak berpotongan, tetapi di luar sesamanya.
2. Bersinggungan di luar
Perhatikan gambar berikut!
Dari gambar di atas diperoleh, jika  =
= 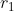 +
+  , maka lingkaran
, maka lingkaran 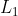 dan lingkaran
dan lingkaran 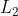 saling bersinggungan .
saling bersinggungan .
3. Lingkaran yang satu di dalam lingkaran lainnya. Kedudukan Lingkaran yang satu di dalam lingkaran lainnya terdiri atas 3 jenis yaitu:
- Lingkaran pertama bersinggungan dengan lingkaran 2 di dalam
- Lingkaran pertama dengan lingkaran 2 sepusat
- Lingkaran pertama tidak bersinggungan dan tidak sepusat dengan lingkaran 2
 |
| Lingkaran pertama bersinggungan dengan lingkaran 2 di dalam |
Dari gambar di atas diperoleh lingkaran 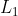 dengan jari-jari
dengan jari-jari 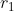 dan lingkaran
dan lingkaran 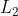 dengan jari-jari
dengan jari-jari  sehingga:
sehingga:
Jadi, jika 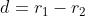 maka lingkaran pertama bersinggungan dengan lingkaran 2 di dalam
maka lingkaran pertama bersinggungan dengan lingkaran 2 di dalam
. Perhatikan gambar berikut!
Perhatikan gambar berikut!
 |
| Lingkaran pertama dengan lingkaran 2 sepusat |
Jadi, jika 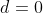 maka Lingkaran pertama dengan lingkaran 2 sepusat
maka Lingkaran pertama dengan lingkaran 2 sepusat
4. Lingkaran berpotongan dengan lingkaran
Perhatikan gambar berikut!
Gambar di atas, disimpulkan bahwa:
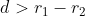 dan
dan 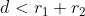
- AB adalah tali busur sekutu
- Sentral
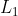
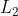 membagi dua tegak lurus tali busur AB
membagi dua tegak lurus tali busur AB - garis tersebut adalah garis kuasa
Jadi, jika 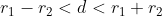 maka
maka Lingkaran pertama berpotongan dengan lingkaran 2
Ingat, dalam menentukan jarak antara pusat lingkaran yaitu  , maka penting dipahamai jarak dua titik
, maka penting dipahamai jarak dua titik \,&space;\,&space;dan\,&space;\,&space;(x_{2},y_{2})) yaitu:
yaitu:
Untuk memahami penjelasan di atas perhatikan contoh soal berikut:
Contoh 1:
Diketahui pusat lingkaran  adalah (2, 6) dengan panjang jari-jari 2 cm. Sedangkan koordinat pusat lingkaran
adalah (2, 6) dengan panjang jari-jari 2 cm. Sedangkan koordinat pusat lingkaran  adalah (10, 0) dengan jari-jari 6 cm. Selidikilah kedudukan antara lingkaran
adalah (10, 0) dengan jari-jari 6 cm. Selidikilah kedudukan antara lingkaran  dan lingkaran
dan lingkaran  !
!
Pembahasan:
Dari soal dapat dilihat apa saja yang diketahui yaitu:
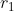 = 2 dan pusat L1 adalah (2,6)
= 2 dan pusat L1 adalah (2,6) = 6 dan pusat L2 adalah (10,0)
= 6 dan pusat L2 adalah (10,0)
sehingga dengan menggunakan konsep jarak dua titik, maka dapat ditentukan jarak kedua titik pusat Lingkaran yaitu d:
^{2}+\left&space;(&space;y_{2}-y_{1}&space;\right&space;)^{^{2}}})
dan
Berdasarkan perhitungan di atas, diperoleh kesimpulan 10 > 8 atau 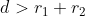 .
.
Contoh 2:
Bagaimanakah kedudukan lingkaran x2 + y2 + 8x -4y – 5 = 0 dan lingkaran x2 + y2 + 4x – 2y – 11 = 0 ?
Pembahasan:
Dari persamaan L1 : x2 + y2 + 8x – 4y – 14 = 0 diperoleh pusat dan jari-jari lingkaran sebgai berikut: Pusat ( -4, 2) dan jari-jari = 5, dan dari persamaan L2 : x2 + y2 + 4x – 2y – 11 = 0 diperoleh pusat dan jari-jari yaitu : Pusat (-2,1) dan jari-jari 4
sehingga dengan menggunakan konsep jarak dua titik, maka dapat ditentukan jarak kedua titik pusat Lingkaran yaitu d:
^{2}+\left&space;(&space;y_{2}-y_{1}&space;\right&space;)^{^{2}}})
&space;\right&space;)^{2}+\left&space;(&space;1-2&space;\right&space;)^{2}})
Berdasarkan perhitungan di atas, diperoleh kesimpulan :  atau .
atau .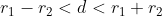
Jadi, jika 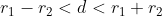 maka lingkaran pertama berpotongan dengan lingkaran 2
maka lingkaran pertama berpotongan dengan lingkaran 2
B. Tali Busur Sekutu
Tali busur lingkaran adalah ruas garis dalam lingkaran yang menghubungkan 2 titik pada lingkaran. Untuk memahami tali busur sekutu, maka coba lihat gambar di bawah ini:
Dengan memperhatikan gambar di atas, maka garis AB adalah tali busur sekutu dari lingkaran 1 dan lingkaran 2.
Jika diketahui:
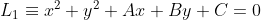
maka persamaan tali busur sekutu AB adalah:
Persamaan lingkaran yang melalui titik A dan B dapat dinyatakan sebagai:
atau
=0) ,
, dimana m adalah parameter
Untuk memahami materi tali busur lihat contoh soalnya di sini:
dengan jari-jari
dan lingkaran
dengan jari-jari
, dimana
>
. Misalkan d = jarak pusat lingkaran
dan
.
maka lingkaran
dan
tidak berpotongan, tetapi di luar sesamanya.
=
+
, maka lingkaran
dan lingkaran
saling bersinggungan .




























Puspa Malem hadir pak
ReplyDeleteVelicia Chinnara Purba
ReplyDeleteHadir pak
nayla faiza hadir pak
ReplyDeleteRisda putri greccella
ReplyDeleteHadir pak
Anggia Rehulina S
ReplyDeleteReza ananda hadir pak
ReplyDeleteAndreas P. M. Simanjuntak
ReplyDeleteHadir pak
Putri Emia Noventa Br Ginting
ReplyDeleteHadir pak
K.Sanjena Jenifer
ReplyDeleteHadir pak
Cindy Azzahra Al Shinta hadir pak
ReplyDeleteChatrin Amelia Gurusinga
ReplyDeleteRezky Gabe
ReplyDeleteCantika
ReplyDeleteXI IA 5
Khayrunnia sindi
ReplyDeleteXI IA 5
This comment has been removed by the author.
ReplyDeleteNesya Adiva
ReplyDeleteXI IA5
ALIFA TSABITA PUTRI
ReplyDeleteXI IA5
Josep Sihombing
ReplyDeleteXI IA5
SINTA INDAH WARDANA XI IA5
ReplyDeleteRamaa Pratamaa XI IA 5
ReplyDeleteTabrisma Dinaya XI IA 5
ReplyDeleteHappy chrisdayanti laia Xl lA 5
ReplyDeleteDerja Diovani XI-IA5
ReplyDeleteYola natasya Ginting XIA 5
ReplyDeleteSiti Annisa
ReplyDeleteXI IA 5
Leonard Chandra XI IA 5
ReplyDelete