Salam Para BintangKali ini kita melanjutkan materi berikutnya yaitu tentang komposisi transformasi geometri . Apkah sudah pernah dengar gak tentang komposisi Transformasi Geometri? Komposisi artinya gabungan dari beberapa elemen atau yang tersusun dari beberapa jenis benda. Komposisi tranformasi hampir mirip dengan komposisi fungsi. Untuk lebih jelasnya, kita bahas materinya secara tuntas.
Sebelum mempelajari komposisi tranformasi, kalian wajib paham dengan materi berikut:
Transformasi Geometri Jenis-Jenisnya dan
Translasi , Refleksi , Rotasi dan Dilatasi
Jika tdak dapat memahami materi di atas, maka dipastikan dalam mempelajari komposisi transformasi akan mengalami kesulitan.
Komposisi Transformasi
Apabila transformasi 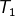 bersesuaian dengan matriks
bersesuaian dengan matriks 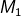 dan transformasi
dan transformasi 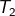 bersesuaian dengan matriks
bersesuaian dengan matriks 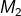 , maka transformasi
, maka transformasi 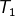 dilanjutkan dengan tranformasi
dilanjutkan dengan tranformasi 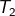 dapat dinyatakan sebagai komposisi transformasi seperti berikut:
dapat dinyatakan sebagai komposisi transformasi seperti berikut:
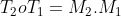
Komposisi transformasi bersifat antikomutatif yang dituliskan dengan : 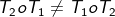
Namun khsusus untuk transformasi translasi berurutan berlaku sifat komutatif karena komposisinya dituliskan sebagai penjumlahan,
Untuk memahami penjelasan tentang rumus-rumus di atas, maka perlu sekali kita berlatih menyelesaikan soal-soalnya. Cek selalu di sini !
Persamaan bayangan kurva y = x² – 2x – 3 oleh rotasi [0, 180°], kemudian dilanjutkan oleh pencerminan terhadap garis y = -x adalah ….
Contoh 2:
Persamaan bayangan dari lingkaran x² +y² +4x – 6y – 3 = 0 oleh transformasi yang berkaitan dengan matriks  adalah….
adalah….
Contoh 3:
T1 dan T2 adalah transformasi yang masing-masing bersesuaian dengan 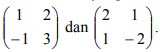 Ditentukan T = T1 o T2 , maka transformasi T bersesuaian dengan matriks…
Ditentukan T = T1 o T2 , maka transformasi T bersesuaian dengan matriks…
Contoh 4:
Ditentukan matriks transformasi .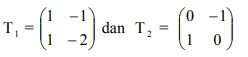 Hasil transformasi titik (2,-1) terhadap T1 dilanjutkan T2 adalah….
Hasil transformasi titik (2,-1) terhadap T1 dilanjutkan T2 adalah….
Contoh 5:
Jika elips 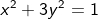 dicerminkan terhadap sumbu x, kemudian digeser 1 ke kiri akan mempunyai persamaan...
dicerminkan terhadap sumbu x, kemudian digeser 1 ke kiri akan mempunyai persamaan...
Contoh 6:
Bayangan titik A(4,1) oleh pencerminan terhadap garis x = 2 dilanjutkan pencerminan terhadap garis x = 5 adalah titik....
Contoh 7:
Diketahui 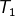 transformasi yang bersesuaian dengan matriks
transformasi yang bersesuaian dengan matriks 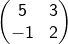 dan
dan 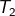 transformasi yang bersesuaian dengan matriks
transformasi yang bersesuaian dengan matriks 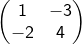 . Bayangan A(m,n) oleh tranformasi
. Bayangan A(m,n) oleh tranformasi 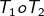 adalah (-9,7). Nilai m + n =.........
adalah (-9,7). Nilai m + n =.........
Contoh 8:
Diberikan 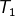 adalah translasi oleh
adalah translasi oleh  dan
dan 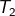 adalah translasi
adalah translasi 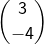 , maka (
, maka ( 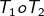 ) (3,5) adalah...
) (3,5) adalah...
Contoh 9:
Persamaan peta kurva y = x² – 3x + 2 karena pencerminan terhadap sumbu x dilanjutkan dilatasi dengan pusat O dan factor skala 3 adalah…
Contoh 10:
Segitiga ABC dengan A(2,1), B(6,1), C(6,4) ditransformasikan dengan matriks transformasi 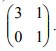 . Luas bangun hasil transformasi segitiga ABC adalah….
. Luas bangun hasil transformasi segitiga ABC adalah…. Untuk pembahasan 1-10, lihat di video ini !
Contoh 11:
Oleh matriks A = 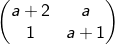 , titik P(1, 2) dan titik Q masing-masing ditransformasikan ke titik P'(2, 3) dan Q'(2,0). Tentukan koordinat titik Q.
, titik P(1, 2) dan titik Q masing-masing ditransformasikan ke titik P'(2, 3) dan Q'(2,0). Tentukan koordinat titik Q.
Contoh 12:
Persamaan peta kurva y = x² – 3x + 2 karena pencerminan terhadap sumbu x dilanjutkan dilatasai dengan pusat O dan factor skala 3 adalah…
Contoh 13:
Pencerminan terhadap sumbu x adalah A, pencerminan terhadap sumbu y adalah B dan rotasi 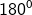 terhadap pusat O adalah H. Tentukan matriks B(A(HA)).
terhadap pusat O adalah H. Tentukan matriks B(A(HA)).
Contoh 14:
Persamaan peta garis 3x – 4y = 12, karena refleksi terhadap garis y – x = 0, dilanjutkan oleh transformasi yang bersesuaian dengan matriks 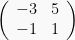 adalah…
adalah…
Contoh 15:
Diketahui persamaan bayangan garis 2x-3y - 5 = 0 yang direfleksikan terhadapa garis y = x, kemudian dilanjutkan oleh matriks
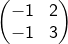
adalah......
Contoh 16:
Persamaan garis y = 3x - 2 dicerminkan terhadap sumbu x, kemudian diputar dengan R [O,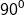
], Persamaan bayangannya adalah........
Contoh 17:
Diketahui bayangan kurva oleh pencerminan terhadap garis y = x, lalu dilanjutkan dengan dilatasi pusat O skala 3 adalah 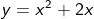 . Persamaan kurva asal adalah.......
. Persamaan kurva asal adalah.......
Contoh 18:
Bayangan kurva 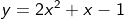 jika dicerminkan pada sumbu x, lalu dilanjutkan dengan rotasi terhadap titik pusat O sejauh
jika dicerminkan pada sumbu x, lalu dilanjutkan dengan rotasi terhadap titik pusat O sejauh 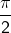 berlawanan arah dengan putaran jam adalah....
berlawanan arah dengan putaran jam adalah....
Contoh 19:
Jika vektor
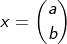
didilatasi sebesar b kali, kemudian dirotasi sejauh
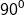
berlawanan arah jarm jam terhadapa titik pusat menjadi vektor y, maka nilai ax-y adalah.........
Contoh 20:
Titik (x,y) ditranslasikan oleh
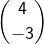
ke titik (2,5). Jika titik (x,y) dicerminkan terhadap suatu garis menghasilkan titik (-8,2) , maka persamaan garis tersebut adalah.....
Contoh 21:
Garis x -2y + 3= 0 ditransformasikan oleh transformasi matriks
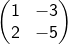
. Tentukan persamaan bayangan garis tersebut.
Contoh 22:
Tentukan bayangan segitiga ABC dengan A(2,1), B(6,1), C(5,3) jika direfleksi terhadap sumbu y, lalu dilanjutkan rotasi (O,
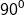
)
Contoh 23:
Luas bayangan segitiga PQR dengan P(1,0), Q(6,0) dan R(6,3) oleh transformasi matriks
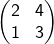
dan dilanjutkan dengan
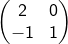
adalah.......
Contoh 24:
Persamaan garis 2x-y+4=0. Jika dicerminkan terhadapa garis y = x, dilanjutkan rotasi berpusat di (0,0) sejauh
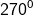
berlawanan arah jarum jam adalah.........
Contoh 25:
Diketahui gradien garis yang melalui titik O(0,0) dan P(a,b) adalah -2. Jika P dicerminkan terhadap sumbu x, kemudian digeser 5 satuan ke bawah dan satu satuan ke kiri, maka bayangannya adalah Q sedemikian sehinggagradien garis melalui Q dan O(0,0) adalah -1. Koordinat titik P adalah....
Contoh 26:
Untuk pembahasan 11-25 ditunggu ya...(Segera Update)
bersesuaian dengan matriks
dan transformasi
bersesuaian dengan matriks
, maka transformasi
dilanjutkan dengan tranformasi
dapat dinyatakan sebagai komposisi transformasi seperti berikut:
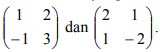 Ditentukan T = T1 o T2 , maka transformasi T bersesuaian dengan matriks…
Ditentukan T = T1 o T2 , maka transformasi T bersesuaian dengan matriks…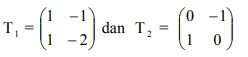 Hasil transformasi titik (2,-1) terhadap T1 dilanjutkan T2 adalah….
Hasil transformasi titik (2,-1) terhadap T1 dilanjutkan T2 adalah…. 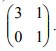 . Luas bangun hasil transformasi segitiga ABC adalah….
. Luas bangun hasil transformasi segitiga ABC adalah….





















Nama:Aser penial sitepu
ReplyDeleteKelas:XI IS 4
Hadir pak
Maya keristina surbakti
ReplyDeleteXl is4
Hadir pak
EWI CLAUDYA BR TARIGAN
ReplyDeleteXI IPS 4
HADIR PAK
Ferdi Octavianus Lim
ReplyDeleteXI IS 4
HADIR PAK
BRIAN CHRISTIAN SIANIPAR
ReplyDeleteXI IPS 4
HADIR PAK